Structure of Materials::Crystal Systems and Bravais Lattice

Crystal Systems and Bravais Lattice

So, now, in this new lecture, we will discuss Crystal Systems and Bravais Lattices. There are 6 crystal family out of them 7 are Crystal System also there are 14 Bravais lattice, 32 points groups and 230 space groups.

Table of Crystal Systems:-

 What have we discussed in previous lectures on which was a background basically on how do you construct a lattice? What do you mean by lattice? And what is the meaning of a crystal lattice?.

What we have seen is, you have a point lattice, and in this point lattice you can make a unit cell, the unit cell has lattice parameters, you can make a crystal lattice by replacing points with atoms or group of atoms. Then we talked about primitive unit cells, but a question is remains in the unit cell is, what kind of unit cell you choose? Can you choose any arbitrary unit cell? Because there are multiple possibilities, for example, let me remove the other ones who are far you can choose this as a unit cell, you can choose this as a unit cell.

So, there are multiple possibilities; the question is, what is the basis for choosing a unit cell? So, that is what we will discuss in the next few lectures. In this lecture, I will tell you the established mechanisms to identify these different patterns, and then we will get into why these patterns, and what is the basis of making these patterns? So, what we have here is we call them is, you cannot choose any arbitrary shape. First of all, the shapes are divided into few categories.

 Moreover, those categories define what we call crystal systems. So, there is a total of 7 crystal systems, and the first one is a cubic crystal system. In a cubic crystal system so, we can say these are the crystal systems in 3D. So, you can ask a question about what about crystal systems in 2D?

So, I will give you some hints at the end of it, and I will hope that you will be able to tell me how many maximum possibilities of crystal systems can exist in 2D. So, let me first give you the examples of 3D, and then we will discuss the origins behind these possibilities.

So, in the cubic crystal system, what you have here is, the lattice is based on the cubic arrangement of points in space. So, every point will follow this kind of cubic arrangement such a way that, a = b = c; α = β = γ = 90o.

So, between a and b, you will have γ, between a and c you will have β, and between b and c, you will have α. So, all these three angles will be equal to 90o. So, the arrangement of points allows you to construct a unit cell, and you will go with that cubic unit cell. Because as we will come to perhaps in the next lecture or a lecture after that, this is symmetry, what do we mean by symmetry, we will see that in the next few lectures.

So, we will choose a cubic structure when it is present and when the symmetry permits it. The second choice of this is a slight distortion of cubic, which is called as tetragonal, so what happens here is your unit cell is slightly distorted. So, basically what you do is that you extend the c or compress this c a little bit as compared to the cubic case so, what happens here is a slight you can say it is a slight distortion of a cube.

                                                        a = b ≠ c, α = β = γ = 90o.

So, it is still an orthogonal system, and the cube is an orthogonal system, tetragonal is an orthogonal system. So, that is the only distinction that you have. So, the next one is a little bit even worse than that.

 The third one is called tetragonal unit cell, and you now change the dimensions along with a, b, and c, all the three directions without changing the angles. So, what you have here is,

                                                        a ≠ b ≠ c, α = β = γ = 90o.

So, it is still orthogonal, but lengths are not at all equal so, this is a third variation that you see in this structure.

The fourth one that we talked about is called hexagonal, in this hexagonal system, what you have here is so, you have a unit cell like this, the angle here is 120o, and these other two angles are 90o. So, the angle between a and b is γ. So, here γ is equal to 120o, what about α and β?.

                                                 α = β = 90o ; γ = 120o and a = b ≠ c.

So, why this is called a hexagonal system? Because when you put three of these unit cells together, they make a hexagon pattern. So, this will be the first one, this the second one so, not a very good drawing, but still, you can probably see what I am trying to do here. So, this will be the next one and before I connect it well enough and then you will have this is the second one, and then you can draw the third one in front. So, the third one would be something like that, and these are the three-unit cells that are drawn so, in a hexagonal pattern, this face will look like a hexagonal face.

 So, that is why it is called a hexagonal system, and now the next one is called as rhombohedral. In the rhombohedral system, a = b = c, but α = β = γ ≠ 90o. So, this is what makes a rhombohedral system.
        So, you can say you can see that it is all of like a cube, but it is not a cube you squeeze the cube in such a fashion so that a = b = c, but α = β = γ ≠ 90o.

So, this is called as rhombohedral, and there are two more types, the first one is called as monoclinic and the second one is called a triclinic.

                                                            a ≠ b ≠ c and α ≠ β ≠ γ 

In the monoclinic case, a = b = c, and α = β = 90o ≠ γ, but it is not necessarily as you can see in the hexagonal case it is necessarily 1200, in this case, it does not have to be a necessary angle, it is just not equal to 90o it can be anything else. In the triclinic case, this is the least symmetric of them, where a ≠ b ≠ c and α ≠ β ≠ γ.

So, these are the crystal systems that you can see in 3D. So, what you have here is. So, this is the cube, and the second one is the tetragonal system, the third one is orthorhombic, the fourth one is monoclinic, you have triclinic, you have rhombohedral.

Rhombohedral often also called as trigonal, a = b = c, but α = β = γ ≠ 900. And this is the hexagonal system. So, this is the basic unit cell in the light green.

So, these are the three crystal systems in 3D. So, I will give you a bit of homework you can get back to me in the next class, or I will discuss that in the next class, that what are the possible crystal systems? So, you have seven crystal systems in 3D.

 

 

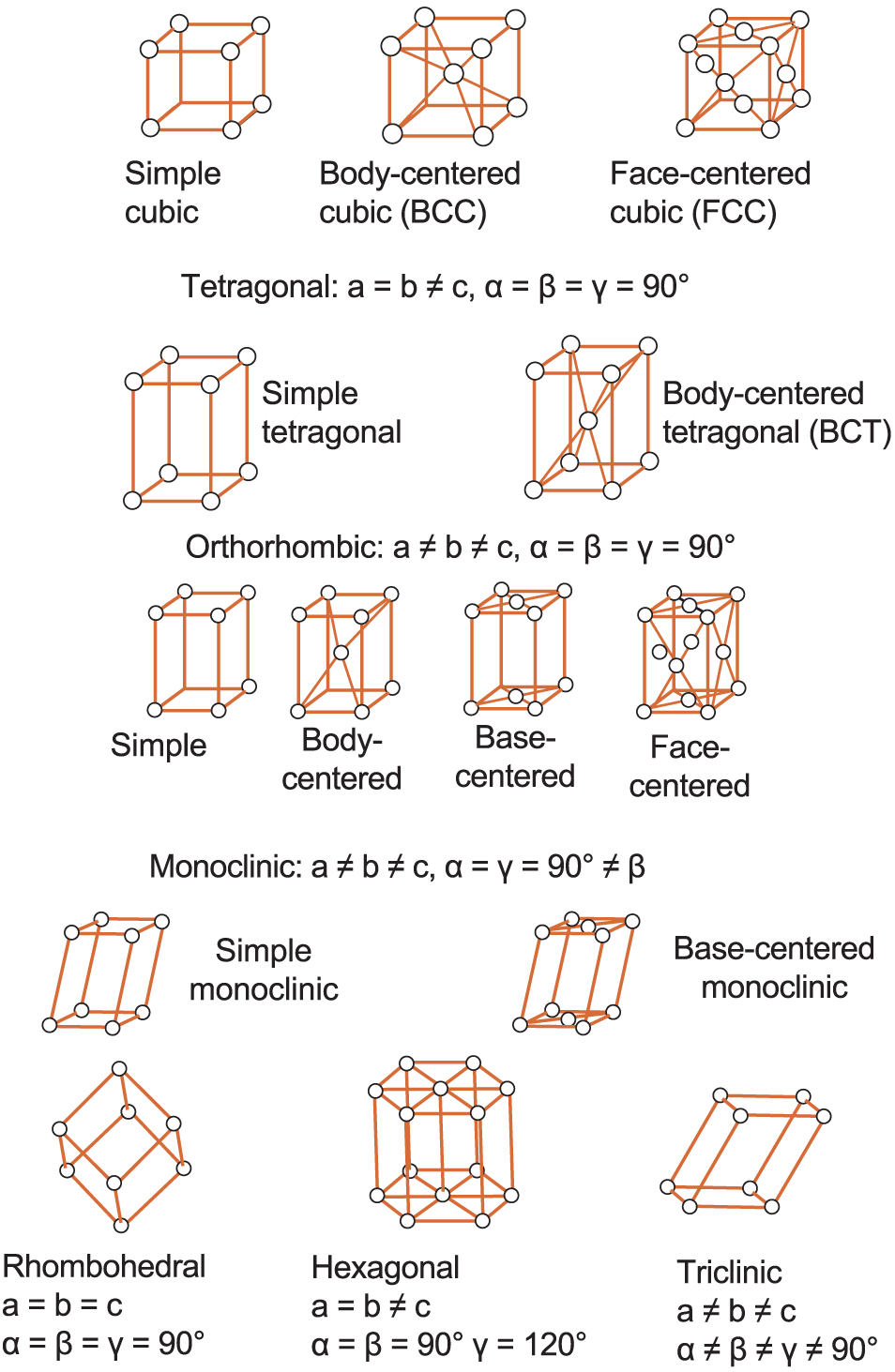
Can you generalize a few crystal systems or possible crystal systems in 3D? So, once you know about the crystal systems, what we talk about now is called Bravais lattices. Bravais lattices are a further up from crystal systems because they now consider whether it is a primitive lattice or whether it is a non-primitive lattice. Again the reason for choosing a particular type of Bravais lattices will be discussed later on when we talk about symmetry, but let us see just based on primitive and non-primitive unit cells what kind of lattices are possible. 

So, in the case of the cubic system, you have three primitive lattices, which are possible, the first one is called as simple cubic lattice that we have seen. So, simple cubic lattice, you can see that how many numbers of atoms does it have? It has only one so, it is a primitive lattice, represented by P, which means primitive anything which is not P is non-primitive.

So, the second possible variant in some in cubic systems is that you can make a bodycentered cubic lattice, where you have one lattice point at the corners, and the second
lattice point is at the center of the unit cell. These two are identical lattice points. So, which means if these were two different atoms, this would not be a body-centered, what will it become? It will become a simple cubic lattice.

So, these two points have to be identical, and if they are identical, then this can be called a body-centered cubic lattice. The third possible variation in the cubic system is face centered cubic lattice, where you have points at the center of each of the faces. So, you have six faces in a cube, and all the six faces will have lattice points at the center of these faces along with corners were being occupied. 

So, the total number of lattice points in this system now becomes four because you have one because you have eight at the corners, which are shared by eight unit cells, 8*(1/8), equal to 1. and then you have six at the faces, but each face is shared by two unit cells, and as a result, you have a total of three. So, you have four identical lattice points. In this case, if any of them becomes different, it does not remain as a face-centered cubic lattice, but they follow the same definition of the cubic crystal system.

The second variation, in this case, is a tetragonal lattice. In the case of tetragonal, c is different from a. So, this is a simple single tetragonal, and you have eight points at the corners, and since you share each of the unit-cell by eight neighbors, eight neighbors share eight unit cells, share one lattice point. And here you have body-centered tetragonal, so you have one lattice point here, both are identical lattice points. So, 8*(1/8), equal to 1, and then you have six at the faces, but each face is shared by two unit cells. So, a total of two. In the previous case, it was (8 * [1/8]) + (6 * [1/6]), which is equal to 4. 

Now, let us see the third example third so, you can always ask me a question, why there is no edge-centered cubic lattice? Why do we not have a face-centered tetragonal? And we will answer those questions, later on, there are crystallographic and symmetry-related reasons, which do not permit the formation of a body-centered tetragonal and facecentered tetragonal lattice. 

So, in the case of tetragonal, there are only two possibilities, simple tetragonal and bodycentered tetragonal, this is primitive, and this is non-primitive. Remember, bodycentered systems are represented as 'I'. So, in the crystallographic terms, any lattice represented as P, which means primitive, I mean body-centered and F means facecentered. So, these are crystallographic notations, which will be useful for you to remember to identify or distinguish between various lattices. 

The third one is called within orthorhombic, and you have four categories simple orthorhombic same as simple cubic and simple tetragonal, so, again, it is P, you have body-centered orthorhombic, which is same as body-centered tetragonal, body-centered  cubic in terms of it is understanding. So, it is I, you have face-centered tetragonal orthorhombic, which is built similarly as you made a face-centered cubic lattice, but within an orthorhombic framework. 

The next one you have is base centered orthorhombic, which means what you have here is on two of the faces, two of the opposing faces you have and an atom or a point sitting at the center of the faces. So, you have one point here, one point here. So, the total number of lattice points, in this case, will be two. 

Now, this option you can see is not available in tetragonal and in cubic and why is it not there that we will discuss later. The next option that we next possible variation that we have is of rhombohedral crystal system. In this case, you have only one lattice, which is called as rhombohedral, although it is a primitive lattice we designated as an R.

So, the primitive lattices of rhombohedral systems are designated as R. in the case of the hexagonal system, only one kind of lattice that is primitive hexagonal. There are other variations that are not possible. In case of monoclinic lattice, you have simple monoclinic which is primitive, and you have base centered monoclinic same as base centered orthorhombic, where you have two opposing faces having atoms so, you have a, b faces two a, b faces have atoms or points at the middle of those faces.

So, this is a base centered, do you need to have a specific two opposing faces? In the case of orthorhombic, it is simple to answer, and it does not need to be only these two faces you can have centers of these faces as atoms. However, monoclinic is not an orthogonal system. So, the question that arises is. 

Can do only these two faces should have atoms at the center of the these, or you can have these also, but only two at a time. So, think about it, and we will answer some of these doubts in the next few lectures. Third and the next to last one is triclinic again. Only a primitive option is possible. So, you can see that there are various primitive lattices and non-primitive lattices that can be built, but only in a few systems in cubic, in tetragonal, in orthorhombic, and in monoclinic, rhombohedral, hexagonal and triclinic do not allow you to have any other possibility.

So, how many of Bravais lattices do you have now? So, you have seven crystal systems, and 14 Bravais lattices. The number of combinations goes down in 2D, there are different numbers, and I will allow you some time to think about it before I give you the answer in the next class. 

So, this is the sort of summary slides you can see that there are 7 crystal systems in case of cubic you have P, I, F, C. P means simple or primitive, I means body-centered, F means face-centered, C means end-centered or side centered or base centered. So, any of these is called C centered. So, you can see the cubic has P, I, F options, but there is no C option, tetragonal has P option, and I option, but there is no F option and C option. Orthorhombic is the most versatile. It allows you to have a primitive lattice, it allows you to have a body centered lattice, it allows you to have a face-centered lattice, and it allows you to have C centered lattice. Again hexagonal is only primitive, trigonal is only primitive, monoclinic is primitive, and C centered triclinic is only primitive.

So, now, the question that arises is, why you do not have this? Let us first discuss these few cases, and once you understand these cases, everything else will become clear about other cases as well. I mean, the only thing that you have to worry about then is probably the monoclinic C case. This will not be possible, but you can see why this is not possible? Because monoclinic is very least symmetry lattice. As a result, it is not possible to make a non-primitive structure because lattice has to be periodic. So, that periodicity of lattice translation symmetry and other symmetry, as we will see later on, should be obeyed.
 

So, the effective number of lattice points now you can calculate. So, for a primitive system, you have only eight corners. So, the number of lattice points is one. For the body-centered system, you have eight corners and one body center. So, the total number of lattice points is two. This gives you the total number of effective atoms in the in itself.

So, the question that we want to answer is, why do we not have 28? Because as we saw in the case of orthorhombic, there are four possibilities. So, why do not we have 28 Bravais lattices? Why do we have only 14 Bravais lattices? So, why some of them are missing? And what is the basis of classification? And the answer is related to their symmetry. So, these answers will lie in symmetry considerations. Symmetry considerations are typically not talked in any of the standard elementary textbooks of material science. So, this you may not find in the references that I have mentioned at the beginning of the lecture series. So, this is something that you may feel a little bit more attentive to, or I will give you some references which are different references to read them about. 

 

So, to summarize, let me go to the last slide, you have a point lattice, which is an ordered array of points with the identical neighborhood. You have a unit cell that is the smallest repeatable unit whose size and shape can be characterized by defining lattice parameters. A crystal lattice can be defined as point lattices with motif or basis this which is an atom or group of atoms. A motif or a lattice point can be either an atom or molecule or a group of atoms or a group of molecules depending on the relative positioning of these atoms and molecules with respect to each other. You define lattice into two different types one is the primitive lattice, second is the non-primitive.

That definition of the primitive lattice is one lattice point per unit cell, and we call it lattice point, not atom because atom is little misleading the moment when you have more than one atom depending upon their relative distribution with respect to each other the definition changes.

So, you may have one atom, and you may have two atoms, you may have three atoms, you may have several molecules within one lattice point. So, that is why we refer it as a one lattice point. So, this is one lattice point per unit cell makes a primitive lattice, and this can be a very big unit cell within a lattice depending upon the relative orientation, and then you can have a non-primitive one which has more than one lattice points per unit cell.

 And then we saw since there are multiple possibilities of the unit cell, it is the smallest repeatable unit. So, the question arises what the possibilities are? Can you have an infinite number of possibilities? So, instead of having the trouble of finding in this system infinite possibilities, let us define certain criteria. That criteria, as you will see, is based on symmetry, it is not an arbitrary criterion. So based on the consideration that we will see later on, there are 7 crystal systems, and based on those 7 crystal systems considering primitive and non-primitive considerations and symmetry considerations, there are 14 Bravais lattices. So, this is the basic introduction to crystallography, in the next few lectures, we will look at what is the underlying reason behind 7 crystal systems and 14 Bravais lattices, and that is where you will also understand the importance of motif or lattice point. That will become clearer as you will as you correlate this so, symmetry. So, we will end up here.

For Next Lecture Click below

Structure of Materials  

 Structure of Materials : Bonding in Materials

Structure of Materials : Correlation between bond and physical properties

 Crystal Structure: Lattice and Basis 

Primitive and Non-primitive Lattices 

Thank you very much

 Click Here : Please Subscribe, Like and Share my channel